공액보법(conjugate beam method)

교재 학습 범위

• 교재 311쪽~317쪽 "7.3.3 공액보법" 예제 7-13까지

공액보법(conjugate beam method)의 원리

• 공액보법은 탄성하중법 또는 탄성중량법(elastic weight method)으로도 불리운다. 비교적 계산이 간단하고 적용범위도 넓다.
• 부재력도 작성을 설명하는 과정에서 얻은 분포하중, 전단력, 휨모멘트의 관계식은 다음과 같다. $$ -w(x)= \frac{dV(x)}{dx} = \frac{d^2M(x)}{dx^2} $$
• 위의 식은 분포하중 \(w(x)\)로부터 발생하는 전단력 \(V(x)\)와 휨모멘트 \(M(x)\)를 계산할 수 있다는 것을 의미하고, 그 계산방법은 이미 학습하였다.
• 한편 탄성곡선법을 설명하는 과정에서 얻은 휨모멘트, 처짐각, 처짐의 관계식은 다음과 같다. $$ - \frac{M(x)}{EI} = \frac{d\theta(x)}{dx} = \frac{d^2y(x)}{dx^2} $$
• 이 식을 분포하중, 전단력, 휨모멘트 관계식과 비교하면, 분포하중 \(w(x)\)가 휨모멘트를 휨강성으로 나눈 \(M(x)/EI\)로, 전단력 \(V(x)\)가 처짐각 \(\theta(x)\)로, 휨모멘트 \(M(x)\)가 처짐 \(y(x)\)로 변경된 것을 제외하면 모두 동일하다는 것을 알 수 있다.
• 즉, \(M(x)/EI\)를 분포하중으로 취급하면 그로부터 계산한 전단력 \(V(x)\)와 휨모멘트 \(M(x)\)가 각각 처짐각 \(\theta(x)\)와 처짐 \(y(x)\)가 된다.

공액보(conjugate beam)

• \(M(x)/EI\)를 분포하중으로 취급하고 그로부터 전단력 \(V(x)\)와 휨모멘트 \(M(x)\)를 계산하기 위해서는 실제 보를 가상의 공액보로 변경해야 한다.
• 공액보는 실제 보의 지점과 절점을 다음과 같이 치환한 것이다.
  • 회전단과 이동단은 그대로 유지
  • 고정단은 자유단으로, 자유단은 고정단으로 치환
  • 부재 내부 회전절점은 부재 내부 이동단으로, 부재 내부 이동단은 부재 내부 회전절점으로 치환

계산절차

1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 M/EI 다이어그램을 작성한다.
2. 실제 보의 지점과 절점을 치환하여 가상의 공액보로 변경한다.
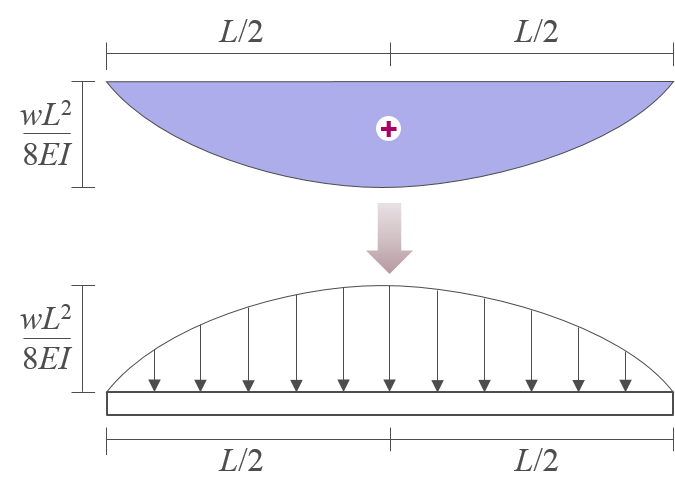
3. \(-\) 부호를 반영하여 M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 공액보에 하중으로 설정한다. 이때 하중은 항상 부재의 축을 향하도록 한다. 다음 그림은 \(+\)의 M/EI 다이어그램과 이를 공액보에 작용하는 하중으로 나타낸 것이다.

   

   다음 그림은 \(-\)의 M/EI 다이어그램과 이를 공액보에 작용하는 하중으로 나타낸 것이다.

   

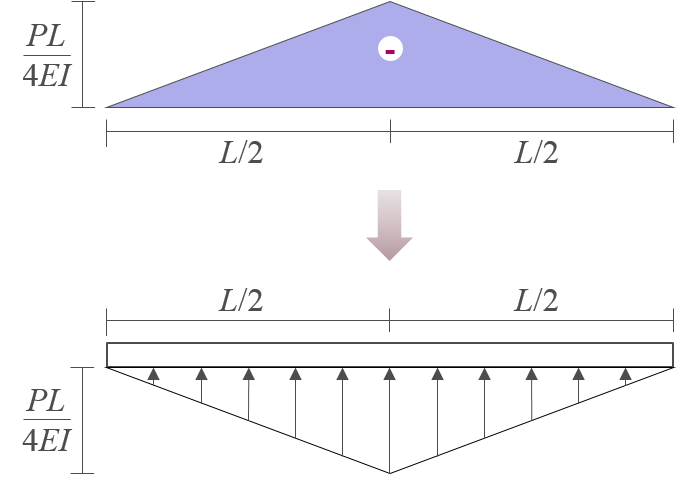
4. 처짐각을 계산할 위치를 가상으로 절단하고 자유물체도를 작성한 후에, 평형조건식을 적용하여 해당 위치의 전단력을 계산한다. 이 값이 해당 위치의 처짐각이다.
5. 처짐을 계산할 위치를 가상으로 절단하고 자유물체도를 작성한 후에, 평형조건식을 적용하여 해당 위치의 휨모멘트를 계산한다. 이 값이 해당 위치의 처짐이다.
6. 앞에서 계산한 전단력이 부재력으로서 \(+\)이면 처짐각은 시계방향, \(-\)이면 반시계방향이다. 그리고 휨모멘트가 부재력으로서 \(+\)이면 처짐은 아래쪽 방향, \(-\)이면 위쪽 방향이다.

예제 1

• 문제 : 공액보법을 이용하여 자유단의 처짐각과 처짐 \(\theta, \, y\)를 계산하시오.

  

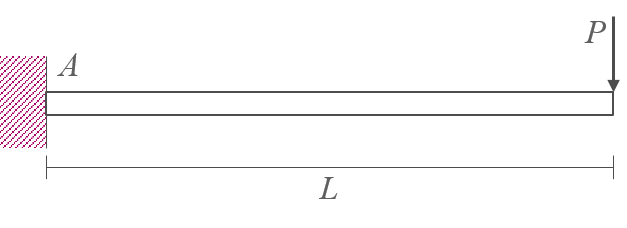
• 풀이
  1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 다음 그림과 같이 M/EI 다이어그램을 작성한다.

     

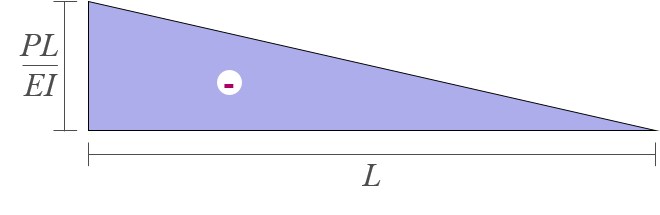
  2. 실제 보의 고정단을 자유단으로, 자유단을 고정단으로 치환하여 다음과 같은 공액보로 변경한다.

     

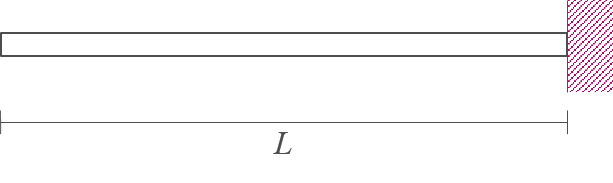
  3. M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 부재의 축을 향하도록 하여 다음과 같이 공액보에 하중으로 설정한다.

     

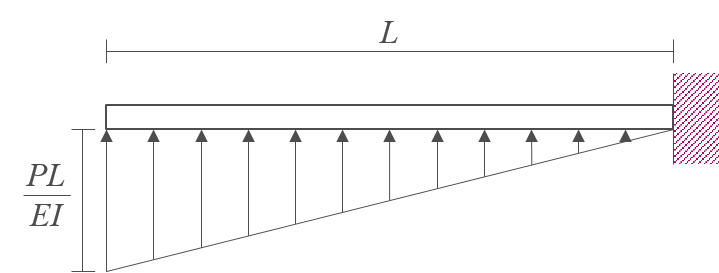
  4. 이 문제에서는 자유단의 처짐각과 처짐을 계산해야 한다. 때문에, 다음과 같이 자유물체도를 그리고 평형조건식을 적용하여 실제 보의 자유단 위치인 공액보의 고정단에 작용하는 전단력 \(V'\)과 휨모멘트 \(M'\)을 계산한다.

     

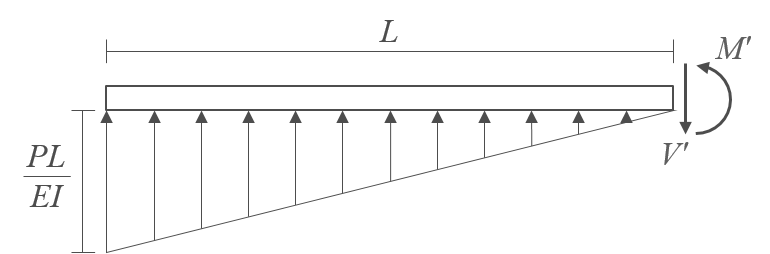
     $$ \Sigma F_y = L \times \frac{PL}{EI} \times \frac{1}{2} - V' = 0; \quad V' = \frac{PL^2}{2EI} \\ \Sigma M_{V'} = -\left( L \times \frac{PL}{EI} \times \frac{1}{2} \right) \times \frac{2L}{3} + M' = 0; \quad M' = \frac{PL^3}{3EI} $$
  5. 자유단의 처짐각 \(\theta\)와 처짐 \(y\)의 크기는 다음과 같다. 그리고, 전단력 \(V'\)과 휨모멘트 \(M'\)이 부재력으로서 \(+\)이므로 처짐각은 시계방향이고 처짐은 아래쪽 방향이다. $$ \theta = \frac{PL^2}{2EI} \quad y = \frac{PL^3}{3EI} $$

예제 2

• 문제 : 공액보법을 이용하여 자유단의 처짐각과 처짐 \(\theta, \, y\)를 계산하시오.

  

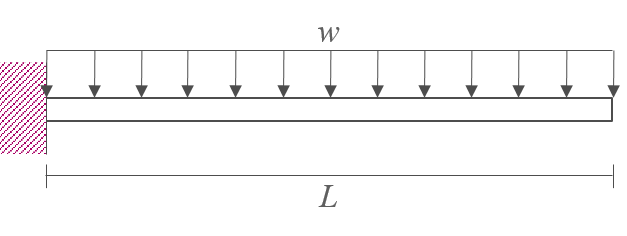
• 풀이
  1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 다음 그림과 같이 M/EI 다이어그램을 작성한다.

     

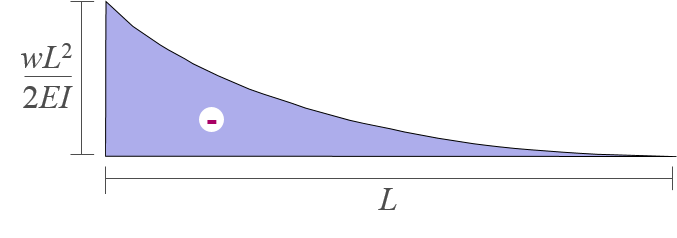
  2. 실제 보의 고정단을 자유단으로, 자유단을 고정단으로 치환하여 다음과 같은 공액보로 변경한다.

     

  3. M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 부재의 축을 향하도록 하여 다음과 같이 공액보에 하중으로 설정한다.

     

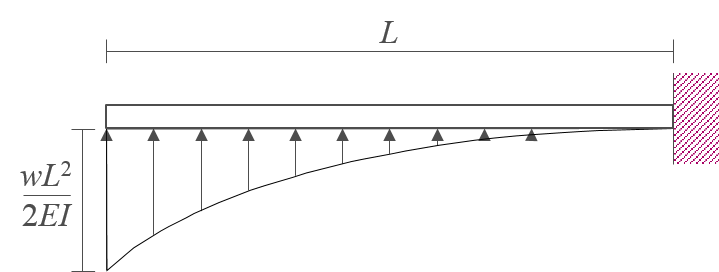
  4. 이 문제에서는 자유단의 처짐각과 처짐을 계산해야 한다. 때문에, 다음과 같이 자유물체도를 그리고 평형조건식을 적용하여 실제 보의 자유단 위치인 공액보의 고정단에 작용하는 전단력 \(V'\)과 휨모멘트 \(M'\)을 계산한다.

     

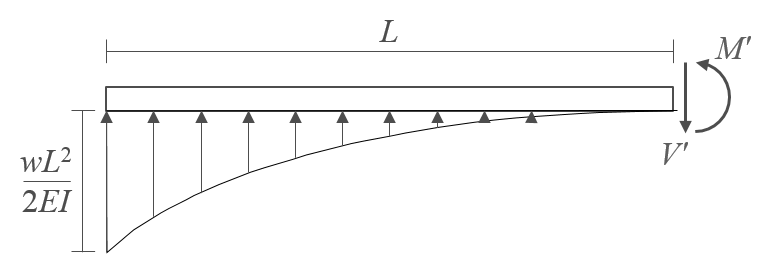
     $$ \Sigma F_y = L \times \frac{wL^2}{2EI} \times \frac{1}{3} - V' = 0; \quad V' = \frac{wL^3}{6EI} \\ \Sigma M_{V'} = -\left( L \times \frac{wL^2}{2EI} \times \frac{1}{3} \right) \times \frac{3L}{4} + M' = 0; \quad M' = \frac{wL^4}{8EI} $$
  5. 자유단의 처짐각 \(\theta\)와 처짐 \(y\)의 크기는 다음과 같다. 그리고, 전단력 \(V'\)과 휨모멘트 \(M'\)이 부재력으로서 \(+\)이므로 처짐각은 시계방향이고 처짐은 아래쪽 방향이다. $$ \theta = \frac{wL^3}{6EI} \quad y = \frac{wL^4}{8EI} $$

예제 3

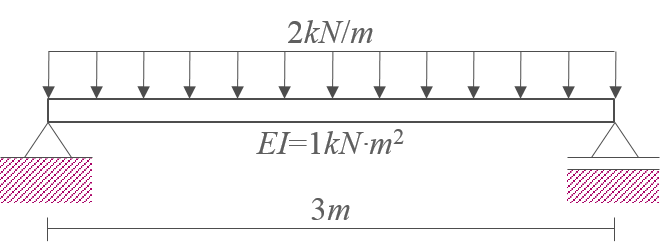
• 문제 : 공액보법을 이용하여 양단의 처짐각과 가운데의 처짐 \(\theta, \, y\)를 계산하시오.

  

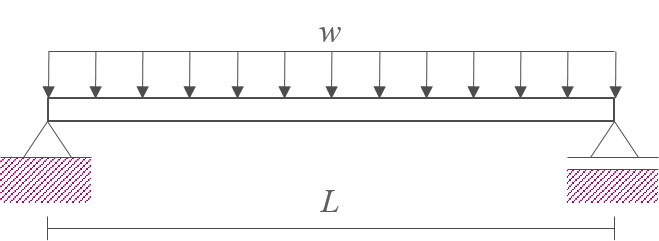
• 풀이
  1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 다음 그림과 같이 M/EI 다이어그램을 작성한다.

     

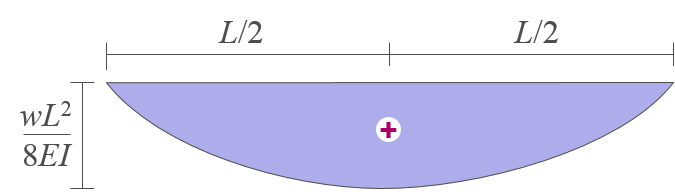
  2. 실제 보가 단순보이므로, 양단의 회전단과 이동단을 그대로 유지한다. 따라서 공액보는 실제 보와 동일하다.
  3. M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 부재의 축을 향하도록 하여 다음과 같이 공액보에 하중으로 설정한다.

     

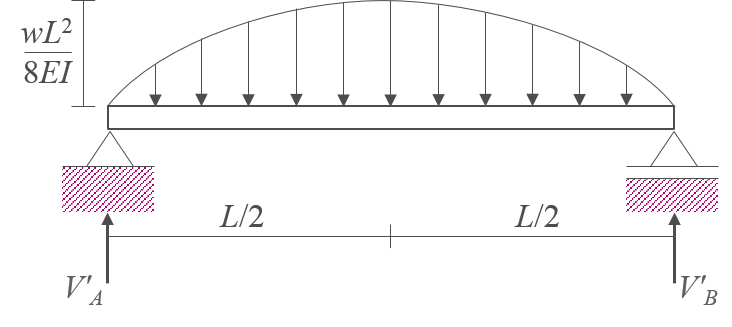
  4. 공액보 전체를 대상으로 자유물체도를 그리고 평형조건식을 적용하여 지점반력 \(V'_A, \, V'_B\)을 다음과 같이 계산한다. $$ \Sigma M_{V'_B} = \left( \frac{L}{2} \times \frac{wL^2}{8EI} \times \frac{2}{3} \times 2 \right) \times \frac{L}{2} - V'_A \times L = 0; \quad V'_A = \frac{wL^3}{24EI} \\ \Sigma F_y = -\left( \frac{L}{2} \times \frac{wL^2}{8EI} \times \frac{2}{3} \times 2 \right) + V'_A + V'_B = 0; \quad V'_B = \frac{wL^3}{24EI} $$
  5. 부재 가운데를 가상으로 절단한 후, 왼쪽 부분을 대상으로 자유물체도를 그리고 평형조건식을 적용하여 다음과 같이 부재 가운데의 휨모멘트를 계산한다.

     

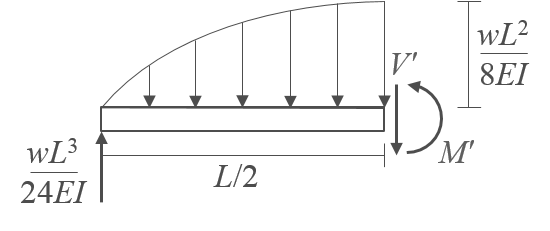
     $$ \Sigma M_{V'} = -\frac{L}{2} \times \frac{wL^3}{24EI} + \left( \frac{L}{2} \times \frac{wL^2}{8EI} \times \frac{2}{3} \right) \times \left( \frac{L}{2} \times \frac{3}{8} \right) + M' = 0; \\ M' = \frac{5wL^4}{384EI} $$
  6. 양단의 처짐각 \(\theta\)와 가운데의 처짐 \(y\)의 크기는 다음과 같다. 그리고, 전단력 \(V'_A\)과 휨모멘트 \(M'\)이 부재력으로서 \(+\)이므로 왼쪽단의 처짐각은 시계방향이고 처짐은 아래쪽 방향이다. 전단력 \(V'_B\)이 부재력으로서 \(-\)이므로 오른쪽단의 처짐각은 반시계방향이다. $$ \theta_A = \frac{wL^3}{24EI} \quad \theta_B = -\frac{wL^3}{24EI} \quad y = \frac{5wL^4}{384EI} $$

예제 4

• 문제 : 공액보법을 이용하여 양단의 처짐각과 가운데의 처짐 \(\theta, \, y\)를 계산하시오.

  

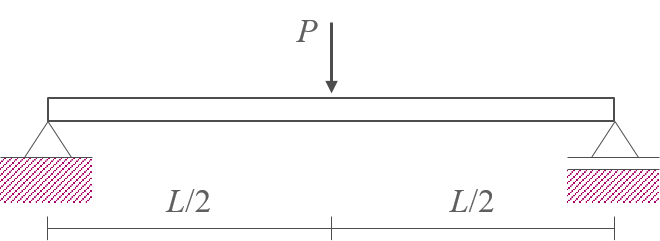
• 풀이
  1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 다음 그림과 같이 M/EI 다이어그램을 작성한다.

     

  2. 실제 보가 단순보이므로, 양단의 회전단과 이동단을 그대로 유지한다. 따라서 공액보는 실제 보와 동일하다.
  3. M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 부재의 축을 향하도록 하여 다음과 같이 공액보에 하중으로 설정한다.

     

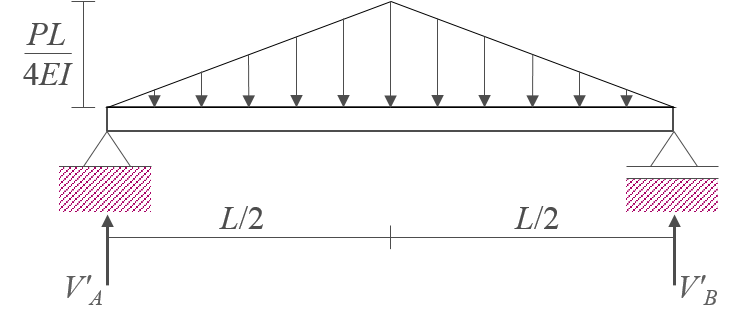
  4. 공액보 전체를 대상으로 자유물체도를 그리고 평형조건식을 적용하여 지점반력 \(V'_A, \, V'_B\)을 다음과 같이 계산한다. $$ \Sigma M_{V'_B} = \left( \frac{L}{2} \times \frac{PL}{4EI} \times \frac{1}{2} \times 2 \right) \times \frac{L}{2} - V'_A \times L = 0; \quad V'_A = \frac{PL^2}{16EI} \\ \Sigma F_y = -\left( \frac{L}{2} \times \frac{PL}{4EI} \times \frac{1}{2} \times 2 \right) + V'_A + V'_B = 0; \quad V'_B = \frac{PL^2}{16EI} $$
  5. 부재 가운데를 가상으로 절단한 후, 왼쪽 부분을 대상으로 자유물체도를 그리고 평형조건식을 적용하여 다음과 같이 부재 가운데의 휨모멘트를 계산한다.

     

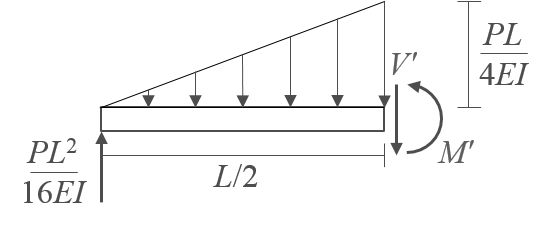
     $$ \Sigma M_{V'} = -\frac{L}{2} \times \frac{PL^2}{16EI} + \left( \frac{L}{2} \times \frac{PL}{4EI} \times \frac{1}{2} \right) \times \left( \frac{L}{2} \times \frac{1}{3} \right) + M' = 0; \\ M' = \frac{PL^3}{48EI} $$
  6. 양단의 처짐각 \(\theta\)와 가운데의 처짐 \(y\)의 크기는 다음과 같다. 그리고, 전단력 \(V'_A\)과 휨모멘트 \(M'\)이 부재력으로서 \(+\)이므로 왼쪽단의 처짐각은 시계방향이고 처짐은 아래쪽 방향이다. 전단력 \(V'_B\)이 부재력으로서 \(-\)이므로 오른쪽단의 처짐각은 반시계방향이다. $$ \theta_A = \frac{PL^2}{16EI} \quad \theta_B = -\frac{PL^2}{16EI} \quad y = \frac{PL^3}{48EI} $$

예제 5

• 문제 : 공액보법을 이용하여 양단의 처짐각과 하중점의 처짐각과 처짐 \(\theta, \, y\)를 계산하시오.

  

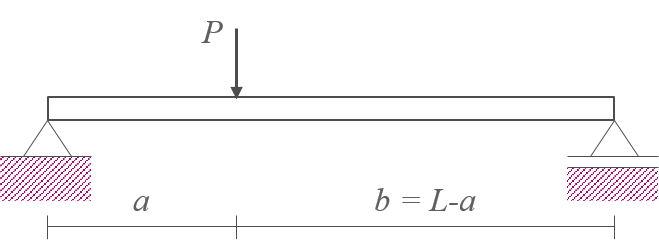
• 풀이
  1. 구조물 전체를 대상으로 자유물체도를 작성하고 평형조건식을 적용하여 지점반력을 계산한다. 이를 바탕으로 다음 그림과 같이 M/EI 다이어그램을 작성한다.

     

  2. 실제 보가 단순보이므로, 양단의 회전단과 이동단을 그대로 유지한다. 따라서 공액보는 실제 보와 동일하다.
  3. M/EI 다이어그램을 \(x\)축에 대칭으로 변환하고 부재의 축을 향하도록 하여 다음과 같이 공액보에 하중으로 설정한다.

     

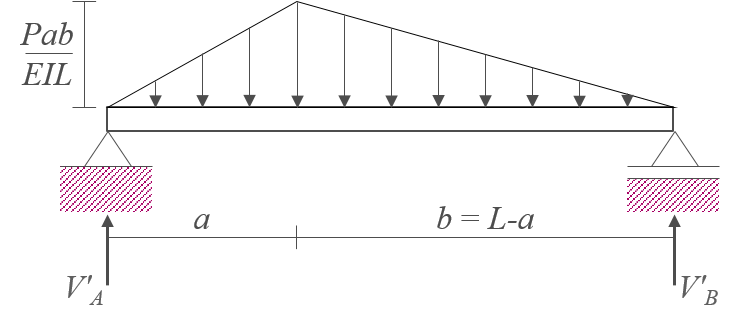
  4. 공액보 전체를 대상으로 자유물체도를 그리고 평형조건식을 적용하여 지점반력 \(V'_A, \, V'_B\)을 다음과 같이 계산한다. $$ \Sigma M_{V'_B} = \left( a \times \frac{Pab}{EIL} \times \frac{1}{2} \right) \times \left( b + \frac{a}{3} \right) + \left( b \times \frac{Pab}{EIL} \times \frac{1}{2} \right) \times \frac{2b}{3} - V'_A \times L = 0; \\ V'_A = \frac{Pab}{6EIL}(L+b) \\ \Sigma M_{V'_A} = -\left( b \times \frac{Pab}{EIL} \times \frac{1}{2} \right) \times \left( a + \frac{b}{3} \right) - \left( a \times \frac{Pab}{EIL} \times \frac{1}{2} \right) \times \frac{2a}{3} + V'_B \times L = 0; \\ V'_B = \frac{Pab}{6EIL}(L+a) $$
  5. 부재의 하중점을 가상으로 절단한 후, 왼쪽 부분을 대상으로 자유물체도를 그리고 평형조건식을 적용하여 다음과 같이 부재 가운데의 전단력과 휨모멘트를 계산한다.

     

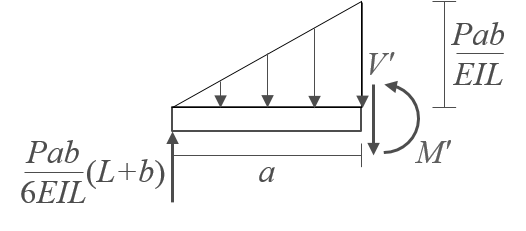
     $$ \Sigma F_y = \frac{Pab}{6EIL}(L+b) - a \times \frac{Pab}{EIL} \times \frac{1}{2} - V' = 0; \quad V' = \frac{Pab}{3EIL}(-a+b) \\ \Sigma M_{V'} = -\frac{Pab}{6EIL}(L+b) \times a + \left( a \times \frac{Pab}{EIL} \times \frac{1}{2} \right) \times \frac{a}{3} + M' = 0; \\ M' = \frac{Pa^2b^2}{3EIL} $$
  6. 양단의 처짐각과 하중점의 처짐각 \(\theta\)와 처짐 \(y\)의 크기는 다음과 같다. 그리고, 전단력 \(V'_A\)과 휨모멘트 \(M'\)이 부재력으로서 \(+\)이므로 왼쪽단의 처짐각은 시계방향이고 처짐은 아래쪽 방향이다. 전단력 \(V'_B\)이 부재력으로서 \(-\)이므로 오른쪽단의 처짐각은 반시계방향이다. 하중점의 처짐각은 \(a, \, b\)의 크기에 따라 부호가 달라지므로 방향을 알 수 없다. $$ \theta_A = \frac{Pab}{6EIL}(L+b) \quad \theta_B = -\frac{Pab}{6EIL}(L+a) \\ \theta = \frac{Pab}{3EIL}(-a+b) \quad y = \frac{Pa^2b^2}{3EIL} $$

복습 퀴즈

1. 다음에서 자유단의 처짐각과 처짐을 계산하려고 한다. M/EI 다이어그램의 전체 면적을 계산하시오.
   
   
2. 퀴즈 1에서 실제 보의 자유단은 공액보에서 무엇으로 치환되는지 쓰시오.
   
3. 퀴즈 1에서 실제 보의 고정단은 공액보에서 무엇으로 치환되는지 쓰시오.
   
4. 퀴즈 1에서 자유단의 처짐각을 계산하시오.
   \(rad\)
5. 퀴즈 1에서 자유단의 처짐을 계산하시오.
   \(m\)
6. 다음에서 왼쪽 끝단의 처짐각과 부재 가운데의 처짐을 계산하려고 한다. M/EI 다이어그램의 전체 면적의 절반을 계산하시오.
   
   
7. 퀴즈 6에서 실제 보의 왼쪽 끝단은 공액보에서 무엇으로 치환되는지 쓰시오.
   
8. 퀴즈 6에서 보의 왼쪽 끝단의 처짐각을 계산하시오.
   \(rad\)
9. 퀴즈 6에서 보의 오른쪽 끝단의 처짐각을 계산하시오.
   \(rad\)
10. 퀴즈 6에서 부재 가운데의 처짐을 계산하시오.
    \(m\)
11. 다음에서 왼쪽 끝단과 하중점 사이의 M/EI 다이어그램의 면적을 계산하시오.
    
    
12. 퀴즈 11에서 오른쪽 끝단과 하중점 사이의 M/EI 다이어그램의 면적을 계산하시오.
    
13. 퀴즈 11에서 실제 보의 오른쪽 끝단은 공액보에서 무엇으로 치환되는지 쓰시오.
    
14. 퀴즈 11에서 왼쪽 끝단의 처짐각을 계산하시오.
    \(rad\)
15. 퀴즈 11에서 오른쪽 끝단의 처짐각을 계산하시오.
    \(rad\)
16. 퀴즈 11에서 하중점에서의 처짐각을 계산하시오.
    \(rad\)
17. 퀴즈 11에서 하중점에서의 처짐을 계산하시오.
    \(m\)